, Where T Is the Solid Tetrahedron With Vertices (0, 0, 0), (1, 0, 0), (1, 1, 0), and (1, 0, 1)

6 . JE *yz dV , where T is the solid tetrahedron with vertices (0,0,0) , (1,0,0), (1,1,0) and (0,0,1)

Get the answer to your homework problem.

Try Numerade Free for 7 Days

Answer

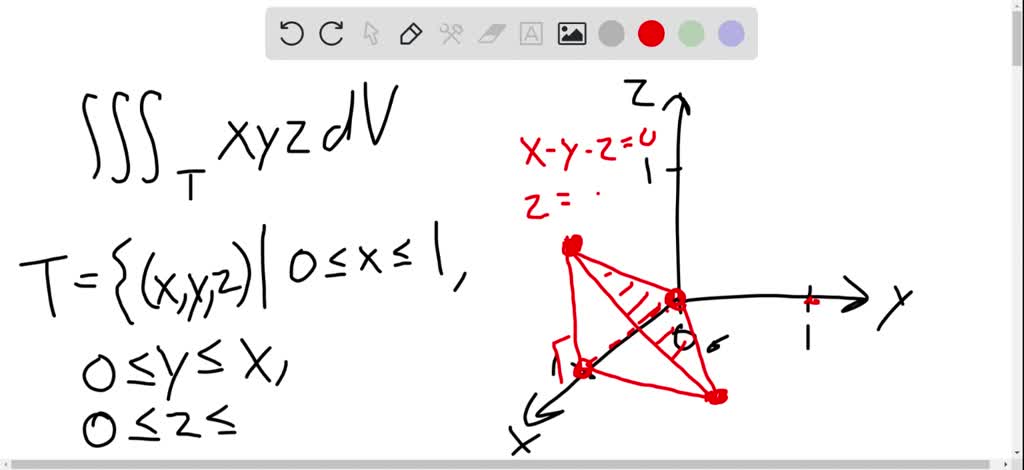
$9-18$ Evaluate the triple integral. $\iiint_{T} x y z d V,$ where $T$ is the solid tetrahedron with vertices $(0,0,0),(1,0,0),(1,1,0),$ and $(1,0,1)$

Discussion

You must be signed in to discuss.

Video Transcript

were given a triple integral and were asked to evaluate it. This is the triple integral over the region t of the function X Y Z TV where t is thes solid tetrahedron which has verte sees 000100110 and 101 This is different from the tetrahedron in the last example. So I'll sketch this first in three space. We have our X y and Z axes we have Vergis is at the origin 100 at 110 just about here and at 101 just about here, Looking them together we get shape that looks like this. So we see that there are two triangular face is facing toward us and then there's also two more behind these. So looking at this shape, we see that the region t can be represented is the set of all triples X y z Such that and I think convenient ways to first notice that X lies between zero and X equals one. If we take this constraint necks, you see that why he's going to lie between zero and y equals X. That's what this line is here And finally we see the Z is going to lie between the X Y plane C zero and this plane here. So this plane that I'm going to shade here in red since this plane is actually vertical in this plane shaded in red, we see this is a point at the origin and has the points 101 and 110 on it. So it satisfies the equation. X minus Why minus Z equals zero. So in other words, X minus Y minus Z equals zero follows it Z is equal to X minus y and so's Eli Between Z equals zero and Z equals X minus y. Now, to evaluate this triple integral, we'll write it as an iterated integral. So we'll integrate first with respect. Dizzy then with respect to y with respect to X. So this is the integral from X equals 0 to 1. Um, why equals zero to y equals X and from why equals Z equals zero to Z equals X minus y of our function. X y z Dizzy D Y d x, and first take the anti derivative With respect to Z, we get them to grow from 0 to 1 zero to x and one half x y z squared zero to x minus. Why d Y d. X substitution gives us integral from 01 zero to x of one half X y times X minus Y squared de y the X which we can expand. This tried it as the integral from 01 from zero x of and we can actually pull out the one half out front so one half times this and then we have X Y times X squared is execute Why minus two x squared y squared plus X y cubed de y DX and then taking the anti derivative with respect to why this is one half integral from 0 to 1 one half execute why squared minus two thirds x squared by a cubed plus 1/4 x y to the fourth zero x dx and evaluating by plugging in for why this gives us one half times the integral from 0 to 1 of one has x cubed times x squared So one half x to the fifth, minus two thirds next to the fifth plus 1/4 next to the fifth DX Miss simplifies to one half times the integral from zero toe one of and combining these coefficients we get 1/12 x to the fifth t X, taking the anti derivative and pulling out factor. We get one half times, 1/12 times 1/6 which is one 144th. Next to the six, they read from 01 And so our answer is 1 144.

, Where T Is the Solid Tetrahedron With Vertices (0, 0, 0), (1, 0, 0), (1, 1, 0), and (1, 0, 1)

Source: https://www.numerade.com/ask/question/6-je-yz-dv-where-t-is-the-solid-tetrahedron-with-vertices-000-100-110-and-001-43569/

Share this post